Дайджест - технический анализ
Леопард Фибоначчи (XII ~ XIIIв. н.э., Италия, Пиза) — один из величайших математиков Средневековья. Именно ему мы обязаны использованием десятичной системы исчисления. В одном из сво их трудов "Книга вычислений" Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римс кой. Мы имеем возможность пользоваться этими преимуществами и по сей день.
И однако же — почему имя великого Фибоначчи неразрывно связано с техническим анализом рынков?
Причина заключается в так называемой числовой последователыности Фибоначчи, состоящей из цифр 1,1,2,3,5,8,13,21,34, 55, 89,144... Фибоначчи открыл се при наблюдении роста потомства у семьи кроликов. Задача была поставлена следующим образом: "Сколько кроликов, помещенных в клетку, можно получить в год от одной пары, если каждая пара производит новую каждый месяц, начиная со второго?" Каждое из чисел последовательности Фибоначчи представляет собой количество пар кроликов в каждый месяц соответственно своему порядковому номеру.
Числовая последовательность Фибоначчи имеет много интересных свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.). Интересующиеся темой особых свойств чисел в последовательности Фибоначчи могут найти ее освещение как в соответствующих математических трудах, так и в некоторых книгах по техническому анализу.
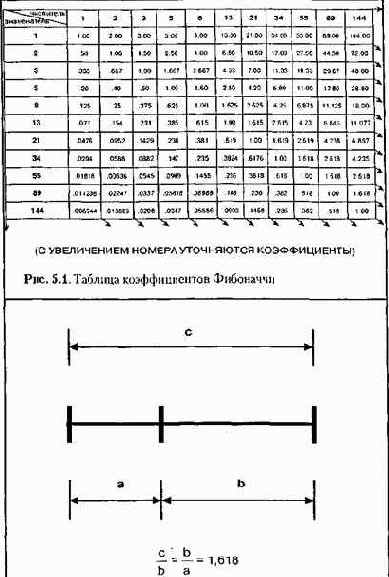
Одним из самых главных следствий этих свойств является существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений различных членов последовательности. Они определяются следующим образом:
Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера (см. таблицу). Отношение же каждого числа к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют ф (фи), и мы поговорим о нем подробнее немного позже.
При делении каждого числа на следующее за ним через одно, получаем число 0.382; наоборот — соответственно 2.618.
Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов:... 4.235,2.618,1.618,0.618, 0.382, 0.236 (рис. 5.1). Упомянем также 0.5 (1/2). Все они играют особую роль в природе, и в частности — в техническом анализе.
Золотое сечение
Числа фибоначчи 2
Числа фибоначчи 3
Определение отрезков времени и использование чисел фибоначчи при установлении длительности циклов
Дуги. Веерные и скоростные линии
Дуги. Веерные и скоростные линии 2
Дуги. Веерные и скоростные линии 3
Использование чисел фибоначчи в анализе ганна
Использование чисел фибоначчи при определении порядка скользящих средних
Использование коэффициентов фибоначчи в волновой теории эллиотта
Основы программирования на языке C
Язык программирования Си был разработан и реализован в 1972 году сотрудником фирмы AT&T Bell Laboratories Денисом Ритчи. Прообразом языка Си для Д. Ритчи послужил язык Би, разработанный Кеном Томпсоном. Он является результатом эволюционного развития языков BCPL (Richards, M., "BCPL: A. Tool for Compiler Writing and System Programming", Proc. AFIPS SJCC, 34, 557-566, 1969) и Би (Johnson, S. C., and B. W. Kernighan, "The Programming Language B", Comp. Sci. Tech. Rep. No. 8, Bell Laboratories. 1973). Основным достоинством языка Си по сравнению с языками BCPL и Би является введение в него типов данных. Язык Си был разработан во время создания операционной системы UNIX (OC UNIX). Развитие языка Си продолжалось и после окончания его разработки и касалось, в частности, проверки типов данных и средств, облегчающих перенос программ в другую среду. Например, разработка проекта переноса OC UNIX на компьютер Interdata 8/32 привела к некоторым добавлениям в язык Си, а именно, к включению в язык таких средств, как объединение (union). Позднее были сделаны попытки включения в язык Си средств абстрагирования данных. В настоящее время рассматривается проект стандарта ANSI C - стандарт языка Си Американского национального института и the C Programming Language - Reference Manual, AT&T Bell Laboratories. С языка Си разработаны совместимые по входному языку трансляторы для 40 типов вычислительных систем, начиная от 8-разрядных микропроцессоров и кончая CRAY-1 - одним из самых мощных в настоящее время суперкомпьютеров. В ходе работ по созданию Мобильного Транслятора с языка Си сам он был переработан для повышения мобильности написанных на нем программ.Достоинства языка Си
Основные типы данных
Основные операции
Выражения
Эквивалентность типов
Ввод и вывод одного символа
Выбор вариантов
Структурное программирование
Создание и использование функций
Классы памяти и область действия
Символические константы: #define
Указатели и массивы
Строковые константы
Определение структурных переменных
Стандартные библиотечные функции
Функция получения случайных чисел
